- Published on
Heaps and Priority Queues
- Authors
- Name
- Curtis Warcup
Table of Contents
Heaps are another category of tree. All the rules that apply to trees will also apply to heaps however, heaps have some special rules.
Binary Heap
Is very similar to a binary search tree, but there are some different rules.
- In a MaxBinaryHeap, the parent nodes are always larger than the child nodes.
- In a MinBinaryHeap, the parent nodes are always smaller than the child nodes.
- In a heap, the parent can have at most two children. However, unlike a tree, there is no order to the children. The children can be either left or right.
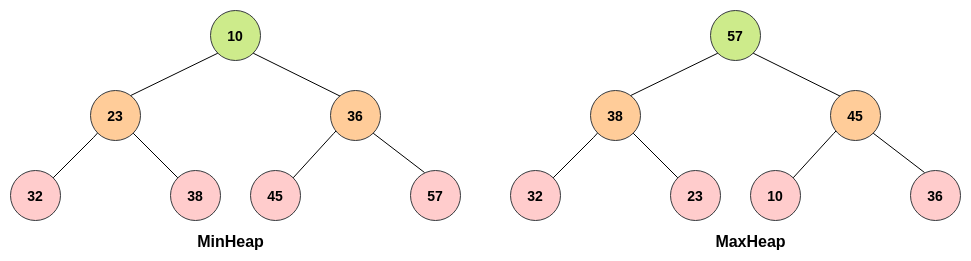
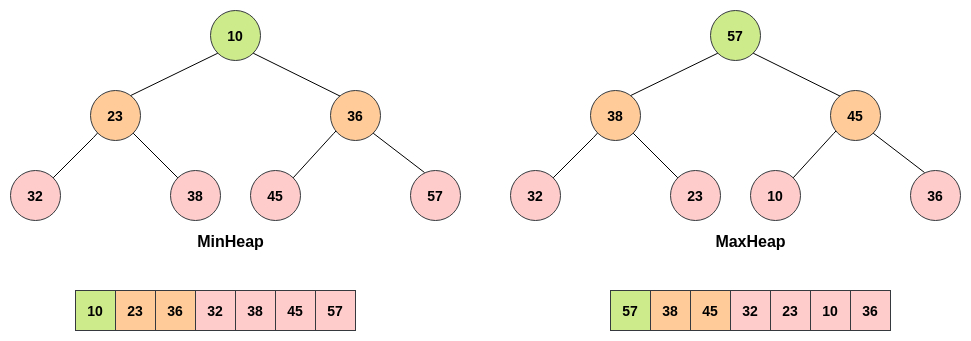
Max Binary Heap
- Each parent has at most two child nodes
- The value of each parent node is always greater than its child nodes
- In a max Binary Heap the parent is greater than the children, but there are no guarantees between sibling nodes.
- A binary heap is as compact as possible. All the children of each node are as full as they can be and left children are filled out first
- The root node is the largest node in the heap
Binary Heaps are used to implement Priority Queues, which are very commonly used data structures
They are also used quite a bit, with graph traversal algorithms
Relationship between Parent and Child in a MaxBinaryHeap
Finding child based off of parent:
- For any index of an array
n...- The left child is stored at
2n + 1 - The right child is stored at
2n + 2
- The left child is stored at
Find the parent using the child node:
- For any child node at index
n... - The parent is stored at
Math.floor((n - 1) / 2)
Class Constructor - MaxBinaryHeap
class MaxBinaryHeap {
constructor() {
this.values = [];
}
Just storing values into an array. We do not need a node class, pointers or a left/right.
Insert - MaxBinaryHeap
Inserting something into the tree is done by push()ing a value to the end of the array. It will most likely NOT be in the correct place. We then need to bubble up the value to the correct place (swap it until it finds the correct place).
Pseudocode:
- add the value to the end of the array
push(). - bubble up (swap value until the value is in the correct spot. Larger values move up).
- compare the value to its parent value using
Math.floor((n-1)/2).- if value is larger, swap parent and value.
- if value is smaller, leave it.
- compare the value to its parent value using
class MaxBinaryHeap {
constructor() {
this.values = []
}
insert(element) {
this.values.push(element)
this.bubbleUp()
}
bubbleUp() {
let index = this.values.length - 1 // keeps track of where the newly added element is.
const element = this.values[index]
while (index > 0) {
let parentIndex = Math.floor((index - 1) / 2) // get index of parent
let parent = this.values[parentIndex] // get parent value
if (element <= parent) break
this.values[parentIndex] = element
this.values[index] = parent
index = parentIndex
}
}
}
let heap = new MaxBinaryHeap()
heap.insert(41)
heap.insert(39)
heap.insert(33)
heap.insert(18)
heap.insert(27)
heap.insert(12)
heap.insert(55)
console.log(heap) // [ 55, 39, 41, 18, 27, 12, 33 ]
ExtractMax() - Removing max element from a heap
- Remove the root.
- Replace root with the most recently added.
- Adjust (sink down)
- Sinking down is the procedure for deleting the root/max element in a heap or the minimum element, and restoring the properties of the heap.
- Is also known as down-heap, bubble down, or heapify down.
Sink Down:
- Compare new root to its children
- Swap larger child with root.
- Continue comparing children and their parent.
- If no larger child exists, then parent is in the correct spot.
Pseudocode ExtractMax():
- Swap the first value in the values property with the last one.
Pop()from the values property, so you can return the value at the end.- Have the new root "sink down" to the correct spot...
- Parent index starts at
0(the root). - Find the index of the left child:
2 * index + 1(make sure its not out of bounds)
- Find the index of the right child:
2 * index + 2(make sure its not out of bounds)
- If the left or right child is greater than the parent element..SWAP.
- If both left and right children are larger, swap with the largest child.
- The child index you swapped to now becomes the new parent index.
- Keep looping and swapping until neither child is larger than the element.
- Return the old root.
- Parent index starts at
// 0 1 2 3 4 5 6 // index
// [ 55, 39, 41, 18, 27, 12, 33 ]
class MaxBinaryHeap {
constructor() {
this.values = []
}
extractMax() {
const max = this.values[0] // get max element, will be the root
const end = this.values.pop() // remove the last element
if (this.values.length > 0) {
this.values[0] = end // set last element as root
this.sinkDown() // sink down the new root
}
return max
}
sinkDown() {
let index = 0 // starts at root
const length = this.values.length
const element = this.values[0]
while (true) {
let leftChildIndex = 2 * index + 1 // get index of left child
let rightChildIndex = 2 * index + 2 // get index of right child
let leftChild, rightChild // initialized, but not declared b/c they may be out of bounds
let swap = null // keeps track of variable we are going to be swapping with
// left side of the heap
if (leftChildIndex < length) {
leftChild = this.values[leftChildIndex] // left child in a variable
if (leftChild > element) {
// compare left child to parent
swap = leftChildIndex
}
}
// right side of the heap
if (rightChildIndex < length) {
rightChild = this.values[rightChildIndex] // right child in a variable
if (
(swap === null && rightChild > element) || // if left child was NOT greater than parent element
(swap !== null && rightChild > leftChild) // OR if left child WAS greater than parent element and right child is greater than left child
) {
swap = rightChildIndex
}
}
if (swap === null) break
// swap
this.values[index] = this.values[swap] // swapping with either the left or right child.
this.values[swap] = element
index = swap
}
}
}
let heap = new MaxBinaryHeap()
heap.insert(41)
heap.insert(39)
heap.insert(33)
heap.insert(18)
heap.insert(27)
heap.insert(12)
heap.insert(55)
console.log(heap) // [ 55, 39, 41, 18, 27, 12, 33 ]
console.log(heap.extractMax()) // 55
console.log(heap) // [ 39, 41, 18, 27, 12, 33 ]
Complete MaxBinaryHeap class
class MaxBinaryHeap {
constructor() {
this.values = []
}
insert(element) {
this.values.push(element)
this.bubbleUp()
}
bubbleUp() {
let index = this.values.length - 1 // keeps track of where the newly added element is.
const element = this.values[index]
while (index > 0) {
let parentIndex = Math.floor((index - 1) / 2) // get index of parent
let parent = this.values[parentIndex] // get parent value
if (element <= parent) break
this.values[parentIndex] = element
this.values[index] = parent
index = parentIndex
}
}
extractMax() {
const max = this.values[0] // get max element, will be the root
const end = this.values.pop() // remove the last element
if (this.values.length > 0) {
this.values[0] = end // set last element as root
this.sinkDown() // sink down the new root
}
return max
}
sinkDown() {
let index = 0 // starts at root
const length = this.values.length
const element = this.values[0]
while (true) {
let leftChildIndex = 2 * index + 1 // get index of left child
let rightChildIndex = 2 * index + 2 // get index of right child
let leftChild, rightChild // initialized, but not declared b/c they may be out of bounds
let swap = null // keeps track of variable we are going to be swapping with
// left side of the heap
if (leftChildIndex < length) {
leftChild = this.values[leftChildIndex] // left child in a variable
if (leftChild > element) {
// compare left child to parent
swap = leftChildIndex
}
}
// right side of the heap
if (rightChildIndex < length) {
rightChild = this.values[rightChildIndex] // right child in a variable
if (
(swap === null && rightChild > element) || // if left child was NOT greater than parent element
(swap !== null && rightChild > leftChild) // OR if left child WAS greater than parent element and right child is greater than left child
) {
swap = rightChildIndex
}
}
if (swap === null) break
// swap
this.values[index] = this.values[swap] // swapping with either the left or right child.
this.values[swap] = element
index = swap
}
}
}
let heap = new MaxBinaryHeap()
heap.insert(41)
heap.insert(39)
heap.insert(33)
heap.insert(18)
heap.insert(27)
heap.insert(12)
heap.insert(55)
console.log(heap) // [ 55, 39, 41, 18, 27, 12, 33 ]
heap.insert(100)
console.log(heap) // [ 100, 55, 41, 39, 27, 12, 33, 18 ]
console.log(heap.extractMax()) // 100
console.log(heap) // [ 55, 39, 41, 18, 27, 12, 33 ]
MinBinaryHeap
class MinHeap {
constructor() {
/* Initialing the array heap and adding a dummy element at index 0 */
this.heap = [null]
}
getMin() {
/* Accessing the min element at index 1 in the heap array */
return this.heap[1]
}
insert(node) {
/* Inserting the new node at the end of the heap array */
this.heap.push(node)
/* Finding the correct position for the new node */
if (this.heap.length > 1) {
let current = this.heap.length - 1
/* Traversing up the parent node until the current node (current) is greater than the parent (current/2)*/
while (current > 1 && this.heap[Math.floor(current / 2)] > this.heap[current]) {
/* Swapping the two nodes by using the ES6 destructuring syntax*/
;[this.heap[Math.floor(current / 2)], this.heap[current]] = [
this.heap[current],
this.heap[Math.floor(current / 2)],
]
current = Math.floor(current / 2)
}
}
}
remove() {
/* Smallest element is at the index 1 in the heap array */
let smallest = this.heap[1]
/* When there are more than two elements in the array, we put the right most element at the first position
and start comparing nodes with the child nodes
*/
if (this.heap.length > 2) {
this.heap[1] = this.heap[this.heap.length - 1]
this.heap.splice(this.heap.length - 1)
if (this.heap.length === 3) {
if (this.heap[1] > this.heap[2]) {
;[this.heap[1], this.heap[2]] = [this.heap[2], this.heap[1]]
}
return smallest
}
let current = 1
let leftChildIndex = current * 2
let rightChildIndex = current * 2 + 1
while (
this.heap[leftChildIndex] &&
this.heap[rightChildIndex] &&
(this.heap[current] > this.heap[leftChildIndex] ||
this.heap[current] > this.heap[rightChildIndex])
) {
if (this.heap[leftChildIndex] < this.heap[rightChildIndex]) {
;[this.heap[current], this.heap[leftChildIndex]] = [
this.heap[leftChildIndex],
this.heap[current],
]
current = leftChildIndex
} else {
;[this.heap[current], this.heap[rightChildIndex]] = [
this.heap[rightChildIndex],
this.heap[current],
]
current = rightChildIndex
}
leftChildIndex = current * 2
rightChildIndex = current * 2 + 1
}
} else if (this.heap.length === 2) {
/* If there are only two elements in the array, we directly splice out the first element */
this.heap.splice(1, 1)
} else {
return null
}
return smallest
}
}
Priority Queue
What is a priority queue?
- A data structure where each element has a priority.
- Elements with higher priorities are removed before elements with lower priorities.
- Fre separate from heaps.
The heap is constructed using priority
- Write a MinBinaryHeap
- lower number means higher priority.
- Each Node has a
valueand apriority. Use thepriorityto build the heap. - Enqueue method accepts a value and priority, makes a new node, and puts it in the right spot based off of its priority.
- Dequeue method removes root element, returns it, and rearranges heap using priority.
In order to make a MinBinaryHeap, we need to add priority and change the comparison < to > signs.
class Node {
constructor(val, priority) {
this.val = val
this.priority = priority
}
}
class PriorityQueue {
constructor() {
this.values = []
}
// accepts a value and priority, makes a new node, and puts it in the right spot based off of its priority.
enqueue(val, priority) {
let newNode = new Node(val, priority)
this.values.push(newNode)
this.bubbleUp()
}
bubbleUp() {
let index = this.values.length - 1
const element = this.values[index]
while (index > 0) {
let parentIndex = Math.floor((index - 1) / 2)
let parent = this.values[parentIndex]
if (element.priority >= parent.priority) break // compare the priority, not the value.
this.values[parentIndex] = element
this.values[index] = parent
index = parentIndex
}
}
dequeue() {
//removes root element, returns it, and rearranges heap using priority.
const min = this.values[0]
const end = this.values.pop()
if (this.values.length > 0) {
this.values[0] = end
// sink down
this.sinkDown()
}
return min
}
sinkDown() {
let index = 0
const length = this.values.length
const element = this.values[0]
while (true) {
let leftChildIndex = 2 * index + 1
let rightChildIndex = 2 * index + 2
let leftChild, rightChild
let swap = null
if (leftChildIndex < length) {
leftChild = this.values[leftChildIndex] // 39
if (leftChild.priority < element.priority) {
swap = leftChildIndex
}
}
if (rightChildIndex < length) {
rightChild = this.values[rightChildIndex] //41
if (
(swap === null && rightChild.priority < element.priority) || // swap never set to left child
(swap !== null && rightChild.priority < leftChild.priority) //
) {
swap = rightChildIndex
}
}
if (swap === null) break
this.values[index] = this.values[swap] // swapping with either the left or right child.
this.values[swap] = element
index = swap
}
}
}
let ER = new PriorityQueue()
ER.enqueue('common cold', 5)
ER.enqueue('gunshot wound', 1)
ER.enqueue('high fever', 4)
ER.enqueue('broken arm', 2)
ER.enqueue('glass in foot', 3)
console.log(ER)
// [ Node { val: 'gunshot wound', priority: 1 },
// Node { val: 'broken arm', priority: 2 },
// Node { val: 'high fever', priority: 4 },
// Node { val: 'common cold', priority: 5 },
// Node { val: 'glass in foot', priority: 3 } ] }
console.log(ER.dequeue()) // Node { val: 'gunshot wound', priority: 1 }
console.log(ER.dequeue()) // Node { val: 'broken arm', priority: 2 }
console.log(ER.dequeue()) // Node { val: 'glass in foot', priority: 3 }
console.log(ER.dequeue()) // Node { val: 'high fever', priority: 4 }
console.log(ER.dequeue()) // Node { val: 'common cold', priority: 5 }
Can see it doesn't matter what order we enqueue. We always dequeue the highest (lower number) priority.
Big O Binary Heaps
| Operation | Time Complexity |
|---|---|
| Enqueue | O(log n) |
| Dequeue | O(log n) |
| Search | O(n) |
Summary
Binary Heaps are very useful data structures for sorting, and implementing other data structures like priority queues.
Binary Heaps are either MaxBinaryHeaps or MinBinaryHeaps with parents either being smaller or larger than their children.
With just a little bit of math, we can represent heaps using arrays!